Phonation onset in a two-layer vocal fold model

Zhaoyan Zhang

The vocal folds are complex layered structures consisting of a muscular layer at the base, multiple layers of lamina propria in the middle, and an outmost epithelium layer. The geometry and mechanical properties of these different layers can be altered by laryngeal adjustments or due to vocal pathologies. Such changes often lead to qualitatively distinct vocal fold vibration and voice quality (Titze, 1994; Colton and Casper, 1996). An ultimate goal of voice production research is to understand and predict the acoustic consequences of such changes in geometry and biomechanical properties of the vocal folds. As a first step, a linear stability analysis was conducted to study the influence of the vocal fold stiffness and geometry on phonation onset in a two-layer body-cover vocal fold model (Zhang, 2009, 2010). The result is briefly described below.

1. Influence of body-cover stiffness ratio

Movies 1 and 2 below show the vocal fold vibration at onset for different body-cover stiffness ratio. Movie 1 is for a case when the vocal fold body is as soft as the vocal fold body. Movie 2 is for a case with a vocal fold body much stiffer than the vocal fold cover.

Comparison of the two movies shows that:
a. Increasing body-cover stiffness ratio gradually restricted the vocal fold motion to the cover layer and the medial surface where the vocal fold motion is the most effective in terms of flow modulation.

b. A wave-like motion was observed for vocal fold surface vibration of small wavelengths, which occurred at high body-cover stiffness ratios or when the vocal fold vibrated at a higher-order mode.

Movie 1: Vocal fold body is as soft as the vocal fold cover

Movie 2: Vocal fold body is much stiffer than the vocal fold cover

2. Competition of coexisting instabilities

For a convergent vocal fold geometry, a sudden jump in phonation onset frequency was observed when the vocal fold body stiffness was gradually increased. Movies 3 and 4 show the vocal fold vibration before and after the frequency jump, when the vocal fold body stiffness was changed from Eb=6 to Eb=7. Comparison of these two movies shows that a slight change in the body stiffness can lead to a qualitative change in the vocal fold vibration pattern and the phonation onset frequency (nearly doubled in this case).

Movie 3: Vocal fold vibration before frequency jump

Movie 4: Vocal fold vibration after frequency jump

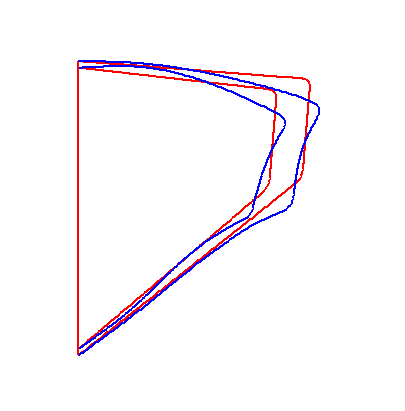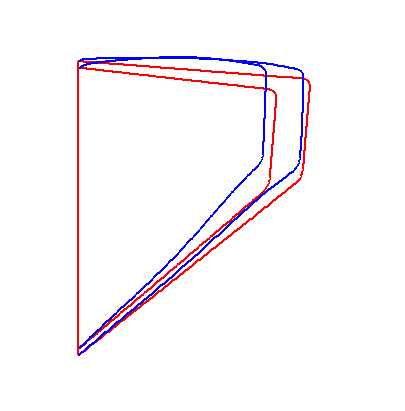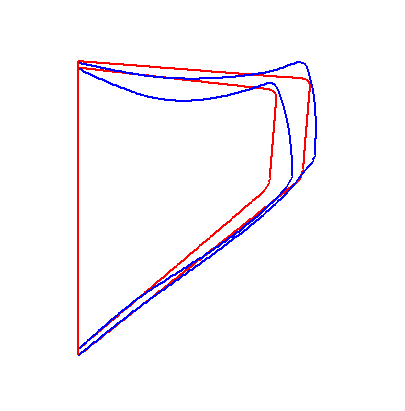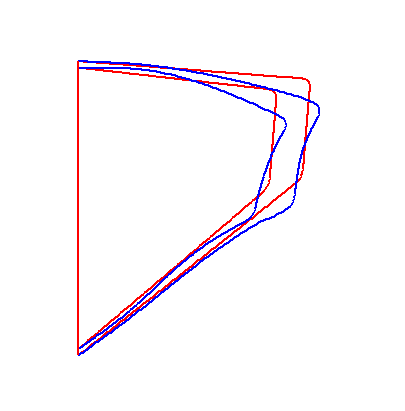
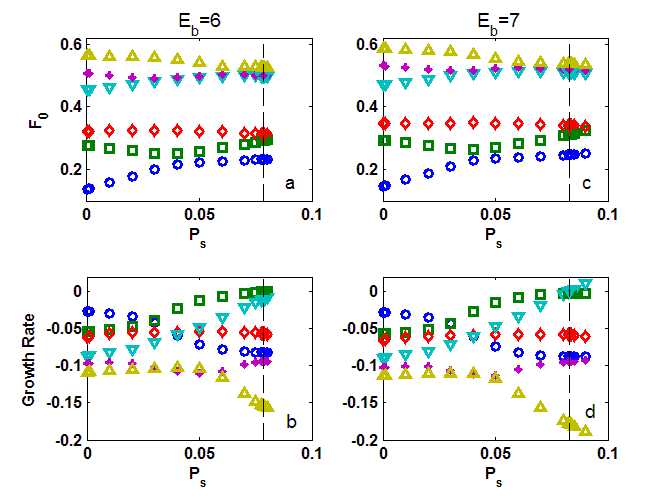
The abrupt increase in vocal fold vibration pattern and phonation onset frequency in response to a slight change in body stiffness was due to the competition of two coexisting instabilities for dominance.  Fig. 1 shows the frequencies and growth rates of the first six eigenvalues of the coupled system for the two cases before (Eb=6) and after (Eb =7) the abrupt increase in F0.  As shown in Fig. 1, there were two groups of eigenmodes of strong interaction: the first group included eigenmodes 1 and 2, and the second group included eigenmodes 4, 5, and possibly 6.  At close to onset, there were two eigenmodes (eigenmode 2 and 4) that had growth rate close to zero and increasing, but with quite different frequencies.  For small values of body stiffness (Eb<7), the interaction between the first two eigenmodes was strong and onset occurred as the second eigenmode first reached zero growth rate.  With increasing body stiffness, this interaction between eigenmodes in the first group gradually weakened, whereas the interaction between eigenmodes of the second group became increasingly stronger.  At certain threshold (Eb=7), the interaction was so strong that the fourth eigenmode reached zero growth rate before the second eigenmode did, leading to an abrupt increase in phonation onset frequency (nearly doubled in this case).

Figure 1: Frequencies and growth rates of the first six eigenvalues of the coupled vocal fold-airflow system as a function of the subglottal pressure. Vertical lines indicate phonation onset.

Although this study focuses on phonation onset, it is reasonable to expect that a similar mechanism may also be present in finite-amplitude vibrations beyond onset, and may play a role in register change.  This mechanism requires that the coupled system have two or more coexisting instabilities so that, given appropriate changes in certain system parameters, the vocal fold vibration can switch from one self-oscillating state to another.  For example, Tokuda et al. (2007) showed that a qualitative change in the vocal fold vibration and phonation frequency in a three-mass model was observed when two synchronizing eigenmodes switched from the first and second eigenmodes to the second and third eigenmodes.  Note that these instabilities could be two near-field FSI instabilities (instabilities due to two pairs of synchronizing eigenmodes, as in the case of Fig. 1), but also could be one near-field FSI instability and one due to the coupling of the vocal fold vibration to sub- or supra-glottal acoustics (Zhang et al., 2006a, b).

This work was supported by NIH/NIDCD research grants No. 1R01DC009229 and No. 1R01DC011299.

References

    Tokuda, I.T., Horacek, J., Svec, J.G., and Herzel, H. (2007), Comparison of biomechanical modeling of register transitions and voice instabilities with excised larynx experiments, J. Acoust. Soc. Am. 122, 519-531.
    Zhang, Z., Neubauer, J., Berry, D. (2006a), The influence of subglottal acoustics in laboratory models of phonation, J. Acoust. Soc. Am. 120, 1558-1569.
    Zhang, Z., Neubauer, J., Berry, D. (2006b), Aerodynamically and acoustically driven modes of vibration in a physical model of the vocal folds, J. Acoust. Soc. Am. 120, 2841-2849. 

Back to Home

UCLA Speech Production Lab

ZHANG,ZHAOYAN 2008